Candidate Key

Candidate Key is a Super Key whose no proper subset is a super key, i.e. suppose if ABC is a candidate key then neither A, B, C or any of its combination can be super key, hence we can say candidate key is a minimal set of attributes of an R( Relational Schema) which can be used to identify a tuple of a table uniquely.

OR

The nominee of Primary Key is a candidate key, for example, Mobile No., Aadhar No., Roll No. all can act as the nominee of Primary key, hence they all are candidate key.

How to determine the Candidate Key

Given a Relational Schema R(X, Y, Z, W) in the following questions determine Super Key and Candidate key.

Example 1: Given R( X Y Z W) and FD= { XYZ → W, XY → ZW and X → YZW

Step 1: Let us calculate the closure of XYZ+ = XYZW (from the method we studied earlier)

Since XYZ closure is determining all the attributes of the table, hence it is Super Key

Step 2: Let us calculate the closure of XY+ = XYZW (from the method we studied earlier)

Since XY closure is determining all the attributes of the table, hence it is Super Key

Step 3: Let us calculate the closure of X+ = XYZW (from the method we studied earlier)

Since X closure is determining all the attributes of the table, hence it is Super Key

As we have talked in the above step only for the super key, not for the candidate key.

Let us see the definition of Candidate Key again (Candidate Key is a Super Key whose no proper subset is a superkey)

From the above definition, XYZ is not a candidate key, as in Step 2 and 3 we found that XY and X are also Super Key (i.e., subset of XYZ are also SK which violate the definition)

XY is not a candidate key, as in Step 3 we found that X is also a Super Key (i.e., subset of XY are also SK which violate the definition)

X is the Candidate key: As X cannot be further subdivided, or X cannot have any subset.

Hence XYZ, XY, and X are all Super Key, while the only X is a candidate key

Example 2: Given R( X Y Z W) and FD= { XY → Z, Z → YW, and W → X }

Step 1: Let us calculate the closure of XY+ = XYZW (from the method we studied earlier)

Since XY closure is determining all the attributes of the table, hence it is Super Key

Step 2: Let us calculate the closure of Z+ = ZYWX (from the method we studied earlier)

Since Z closure is determining all the attributes of the table, hence it is Super Key

Step 3: Let us calculate the closure of W+ = WX (from the method we studied earlier)

Since X closure is not determining all the attributes of the table, hence it is Not Super Key, since it is not SK it can never be Candidate key

As we have talked in the above step only for the super key, not for the candidate key.

Let us see the definition of Candidate Key again (Candidate Key is a Super Key whose no proper subset is a superkey)

From the above definition XY is a candidate key, as in Step 2 and 3 none of the subsets of XY i.e. either X or Y is Super Key.

Z is the Candidate key: As Z cannot be further subdivided, or Z cannot have any subset.

Hence XY and Z are Super Key, also XY and Z are a candidate key

Example 2: Given R( X Y Z W) and FD= { Y → XZW, XZW → Y }

Step 1: Let us calculate the closure of Y+ = XYZW (from the method we studied earlier)

Since Y closure is determining all the attributes of the table, hence it is Super Key

Step 2: Let us calculate the closure of XZW+ = XZWY (from the method we studied earlier)

Since a closure is determining all the attributes of the table, hence it is Super Key

As we have talked in the above step only for the super key, not for the candidate key.

Let us see the definition of Candidate Key again (Candidate Key is a Super Key whose no proper subset is a superkey)

From the above definition, Y is candidate key, As Y cannot be further subdivided, or Y cannot have any subset.

XZW is Candidate key: As no proper subset of XZW is super Key

Hence Y and XZW are Super Key, also Y, and XZW are also a candidate key.

SHORTCUT TO FIND CANDIDATE KEY

Example 1: Give R(X, Y, Z, W) and Set of Functional Dependency FD = { X → Y, Y → Z, Z → X}. The question is to calculate the candidate key and no. of candidate key in above relation R using a given set of FDs.

Let us construct an arrow diagram on R using FD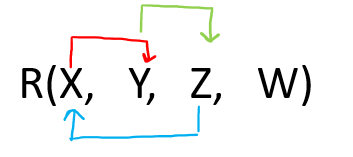

From the above arrow diagram on R, we can see that an attribute W is not determined by any of the given FD, hence W will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have W compulsory attribute.

Let us calculate the closure of W

W + = W (from the method we studied earlier)

Since, closure of W contains only W, hence it is not a candidate key.

Let us check the combination of W, i.e. WX, WY, WZ.

a) W X + = W X Y Z ( from the method we studied earlier)

Since the closure of WX contains all the attributes of R, hence WX is Candidate Key

b) W Y + = W Y Z X (from the method we studied earlier)

Since the closure of WX contains all the attributes of R, hence WY is Candidate Key

c) W Z + = W Z X Y (from the method we studied earlier)

Since the closure of WX contains all the attributes of R, hence WZ is Candidate Key

From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key)

We can say that any further combination of WX, WY, WZ, i.e. WXY, WXYZ, WYZ, WZX will be Super Key but not a candidate key.

Therefore, there are THREE Candidate keys WX, WY, WZ.

Example 2: Give R(X, Y, Z, W) and Set of Functional Dependency FD = { XY → ZW, W → X}. The question is to calculate the candidate key and no. of candidate key in above relation R using a given set of FDs.

Let us construct an arrow diagram on R using FD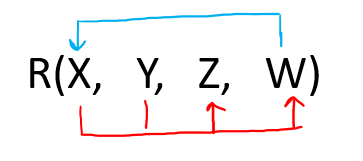

From above arrow diagram on R, we can see that an attribute Y is not determined by any of the given FD, hence Y will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have Y compulsory attribute.

Let us calculate closure of Y

Y+ = Y( from the method we studied earlier)

Since the closure of Y contains the only Y, hence it is not a candidate key.

Let us check the combination of Y, i.e. YX, YW, YZ.

d) Y X + = Y X Z W (from the method we studied earlier)

Since the closure of YX contains all the attributes of R, hence YX is Candidate Key

e) Y W + = Y W X W (from the method we studied earlier)

Since the closure of YW contains all the attributes of R, hence YW is Candidate Key

f) Y Z + = Y Z (from the method we studied earlier)

Since the closure of Y Z contains only Y Z, hence YZ is Not Candidate Key

From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key)

We can say that any further combination of Y X, Y W, will be Super Key but not a candidate key.

Since Y Z is still not candidate key, let us try its combination

Y Z W (Not Allowed, as Y W is already CK)

Y Z X (Not Allowed, as YX is already CK)

Hence any combination of YZ is not allowed.

Therefore, there are TWO Candidate key Y X, Y W.

Example 3: Give R( P, Q, R, S, T, U) and Set of Functional Dependency FD = { PQ → R, R → S, Q → PT}. The question is to calculate the candidate key and no. of candidate key in above relation R using a given set of FDs.

Let us construct an arrow diagram on R using FD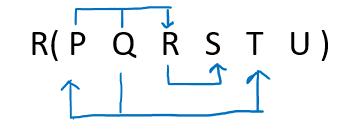

From above arrow diagram on R, we can see that an attribute QU is not determined by any of the given FD, hence QU will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have QU compulsory attribute.

Let us calculate closure of QU using FD = { PQ → R, R → S, Q → PT}.

QU+ = QUPTRS (from the method we studied earlier)

Since the closure of QU contains all the attributes of R, hence it is QU Candidate Key.

From the definition of Candidate Key(Candidate Key is a Super Key whose no proper subset is a Super key)

We can say that any further combination of QU, i.e. QUP, QUR, QUS, QUT, etc.

will be Super Key but not a candidate key.

Therefore. there is only ONE Candidate key QU.

Example 4: Give R(A, B, C, D) and Set of Functional Dependency FD = { AB → CD, C → A, D → B}. The question is to calculate the candidate key and no. of candidate key in above relation R using a given set of FDs.

Let us construct an arrow diagram on R using FD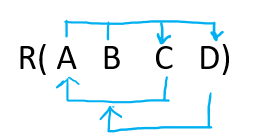

From the above arrow diagram on R, we can see that there is none of the attributes in R which are undetermined, i.e. all attribute in R is determined by anyone of the FD. Now there is confusion as this example is not at all similar to the above three examples.

Hence for such type of questions, we first check the closure of all attributes individually, then their combination by keeping in mind the definition of Candidate Key.

Let us calculate closure of A, B, C, D using FD = { AB → CD, C → A, D → B}

1. A + = A (from the method we studied earlier)
   Since the closure of A contains only A, hence it is not a candidate key.
2. B + = B (from the method we studied earlier)
   Since the closure of B contains only B, hence it is not a candidate key.
3. C + = C A (from the method we studied earlier)
   Since the closure of C contains only C A, hence it is not a candidate key.
4. D + = D B (from the method we studied earlier)
   Since the closure of D contains only D B, hence it is not a candidate key.

Since from above none of the above are candidate key, hence we try the combination of A, B, C, and D i.e. ( AB, AC, AD, BC, BD, CD)

Let us calculate closure of AB, AC, AD, BC, BD, CD using FD = { AB → CD, C → A, D → B}

1. A B + = A B C D (from the method we studied earlier)
   Since the closure of AB contains only all the attributes of R, hence AB is candidate key.
2. A C + = A C (from the method we studied earlier)
   Since the closure of AC contains only AC, hence it is not a candidate key.
3. A D+ = A D B C (from the method we studied earlier)
   Since, closure of AD contains only all the attributes of R, hence AD is candidate key.
4. B C + = B C A D (from the method we studied earlier)
   Since closure of BC contains only all the attributes of R, hence BC is candidate key.
5. B D + = B D (from the method we studied earlier)
   Since the closure of BD contains only BD, hence it is not a candidate key
6. C D + = C D A B
   Since the closure of CD contains only all the attributes of R, hence CD is candidate key.

Since AC and BD are the two combinations which do not form candidate key, therefore let us try their combinations, by keeping in mind that any proper subset of that combination should not be candidate key, as per the definition of a candidate key.

The combination of AC & BD are ACB, ACD, BDA, and BDC but unfortunately, a subset of all combinations is already Candidate Key, hence none of the combinations ( ACB, ACD, BDA, and BDC ) qualify for Candidate key.

Therefore, there are FOUR Candidate Keys: AB, AD, BC, and CD