-
DBMS Tutorial
- dbms-tutorial
- what-is-database
- types-of-databases
- what-is-rdbms
- dbms-vs-rdbms
- dbms-vs-file-system
- dbms-architecture
- three-schema-architecture
- data-models
- data-model-schema
- data-independence
- dbms-language
- acid-properties-in-dbms
Data modeling
- er-model-concept
- notation-for-er-diagram
- er-design-issues
- mapping-constraints
- dbms-keys
- dbms-generalization
- dbms-specialization
- dbms-aggregation
- convert-er-into-table
- relationship-of-higher-degree
Relational data Model
- relational-model-concept
- relational-algebra
- join-operation
- integrity-constraints
- relational-calculus
Normalization
- functional-dependency
- inference-rule
- dbms-normalization
- dbms-1nf
- dbms-2nf
- dbms-3nf
- dbms-bcnf
- dbms-4nf
- dbms-5nf
- relational-decomposition
- multivalued-dependency
- join-dependency
- inclusion-dependence
- canonical-cover
Transaction Processing
- transaction
- transaction-property
- states-of-transaction
- dbms-schedule
- testing-of-serializability
- conflict-schedule
- view-serializability
- recoverability-of-schedule
- failure-classification
- log-based-recovery
- dbms-checkpoint
- deadlock-in-dbms
Concurrency Control
- concurrency-control
- lock-based-protocol
- time-stamping-protocol
- validation-based-protocol
- thomas-write-rule
- multiple-granularity
- recovery-concurrent-transaction
File organization
- file-organization
- sequential-file-organization
- heap-file-organization
- hash-file-organization
- b+-file-organization
- dbms-isam
- cluster-file-organization
Indexing and B+ Tree
Hashing
RAID
Misc
- decomposition-algorithms
- storage-system-in-dbms
- data-dictionary-storage
- file-organization-storage
- selection-of-raid-levels
- bitmap-indexing
- buffer-replacement-strategies
- database-buffer
- estimating-query-cost
- query-processing-in-dbms
- evaluation-of-expressions
- external-sort-merge-algorithm
- hash-join-algorithm
- materialization-in-query-processing
- merge-join-algorithm
- nested-loop-join-algorithm
- selection-operation-in-query-processing
- double-pipelined-join-algorithm
- implementation-of-pipelining
- pipelining-in-query-processing
- advanced-query-optimization
- transforming-relational-expressions
- candidate-key
- closure-of-an-attribute
- questions-on-boyce-codd-normal-form
- questions-on-normalization
- questions-on-third-normal-form
- equivalence-of-functional-dependency
- referential-integrity-constraint
- questions-on-lossy-and-lossless-decomposition
- lossy-or-lossless-decomposition-(second-method)
- questions-to-identify-normal-form
- types-of-relationship-in-database-table
- candidate-key-in-dbms
- primary-key-in-dbms
- super-key-in-dbms
- alternate-key-in-dbms
- composite-key-in-dbms
- foreign-key-in-dbms
- surrogate-key-in-dbms
- unique-key-in-dbms
- purpose-of-normalization
- commit-vs-rollback-in-sql
- ddl-vs-dml
- denormalization-in-databases
- er-model-vs-relational-model
SQL Introduction
- sql-introduction
- characteristics-of-sql
- advantage-of-sql
- sql-datatype
- sql-command
- sql-operator
- sql-table
- sql-select-statement
- sql-insert-statement
- sql-update-statement
- sql-delete-statement
- sql-view
- sql-index
- sql-sub-queries
- sql-clauses
- sql-aggregate-function
- sql-join
- sql-set-operation
DBMS MCQ
Interview Questions
QUESTIONS TO IDENTIFY NORMAL FORMTo solve the question to identify normal form, we must understand its definitions of BCNF, 3 NF, and 2NF: Definition of 2NF: No non-prime attribute should be partially dependent on Candidate Key. i.e. there should not be a partial dependency from X → Y. Definition of 3NF: First, it should be in 2NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e. Y is not a subset of X) then
Definition of BCNF: First, it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then
NOTE: If a table is in BCNF then it is in 3NF, 2NF, and 1NF, similarly if the table is in 3NF Then it is in 2NF and 1NF. Hence, we can say that if a table is in the higher normal form then by default it is in lower normal form.Question 1: Given a relation R( P, Q, R, S, T, U, V, W, X) and Functional Dependency set FD = { PQ → R, QS → TU, PS → VW, and P → X }, determine whether the given R is in which normal form? Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key. 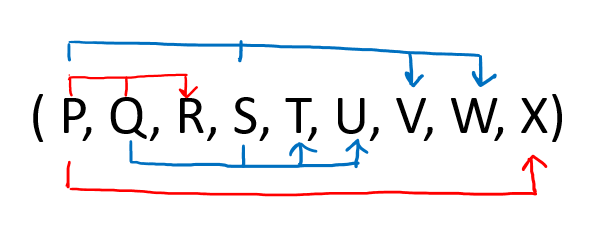 From the above arrow diagram on R, we can see that an attribute PQS is not determined by any of the given FD, hence PQS will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have PQS compulsory attribute. Let us calculate the closure of PQS PQS + = P Q R S T U X V W (from the closure method we studied earlier) Since the closure of PQS contains all the attributes of R, hence PQS is Candidate Key From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key) Since all key will have PQS as an integral part, and we have proved that PQS is Candidate Key, Therefore, any superset of PQS will be Super Key but not a Candidate key. Hence there will be only one candidate key PQS Since R has 9 attributes: - P, Q, R, S, T, U, V, W, X, and Candidate Key is PQS, Therefore, prime attributes (part of candidate key) are P Q and S while a non-prime attribute is R T U V W X Given FD are { PQ → R, QS → TU, PS → VW, and P → X } and Super Key / Candidate Key is PQS NOTE: To solve such questions, we apply reverse engineering, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.
Hence from the above three statements, we can say that table R ( P, Q, R, S, T, U, V, W, X) is in 1NF only. Question 2: Given a relation R( P, Q, R, S, T, U, V, W ) and Functional Dependency set FD = { PQ → R, P → ST, Q → U, and U → VW }, determine given R is in which normal form? Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key. 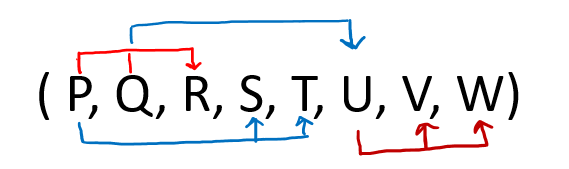 From the above arrow diagram on R, we can see that an attribute PQ is not determined by any of the given FD, hence PQ will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have PQ compulsory attribute. Let us calculate the closure of PQ PQ + = P Q R S T U V W (from the closure method we studied earlier) Since the closure of PQ contains all the attributes of R, hence PQ is Candidate Key From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key) Since all key will have PQ as an integral part, and we have proved that PQ is Candidate Key, Therefore, any superset of PQ will be Super Key but not Candidate key. Hence there will be only one candidate key PQ Since R has 8 attributes: - P, Q, R, S, T, U, V, W and Candidate Key is PQ. Therefore, prime attribute (part of candidate key) are P and Q while a non-prime attribute is R S T U V W Given FD are { PQ → R, P → ST, Q → U, and U → VW } and Super Key / Candidate Key is PQ NOTE: To solve such questions, we apply reverse engineering, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.
Hence from the above three statements b, c, and d we can say that table R ( P, Q, R, S, T, U, V, W, ) is in 1NF only. Question 3: Given a relation R( P, Q, R, S, T, U ) and Functional Dependency set FD = { PQ → R, SR→ PT, T → U }, determine given R is in which normal form? Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key. 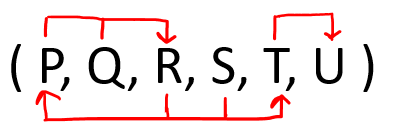 From the above arrow diagram on R, we can see that an attribute QS is not determined by any of the given FD, hence QS will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have QS compulsory attribute. Let us calculate the closure of QS QS + = QS (from the closure method we studied earlier) Since closure QS does not contain all the attributes of R, hence QS is not the Candidate key. On making a combination of QS with another attribute, we found that PQS and RQS determine all the attributes of R, hence PQS and RQS are candidate keys of R. Since R has 6 attributes: - P, Q, R, S, T, U and Candidate Key is PQS and RQS, Therefore, prime attributes (part of candidate key) are P Q R and S while a non-prime attribute is T U Given FD are { PQ → R, SR→ PT, T → U } and Super Key / Candidate Key is PQS and RQS NOTE: To solve such questions, we apply reverse engineering, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.
Hence from the above two statements c and d, we can say that table R ( P, Q, R, S, T, U) is in 1NF only. Question 4: Given a relation R( P, Q, R, S, T) and Functional Dependency set FD = { QR → PST, S → Q }, determine given R is in which normal form? Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.  From the above arrow diagram on R, we can see that an attribute R is not determined by any of the given FD, hence R will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have R compulsory attribute. Let us calculate the closure of R R + = R (from the closure method we studied earlier) Since closure R does not contain all the attributes of R, hence R is not Candidate key. On making a combination of R with another attribute, we found that RS and RQ determine all the attributes of R, hence RS and RQ are candidate keys of R. 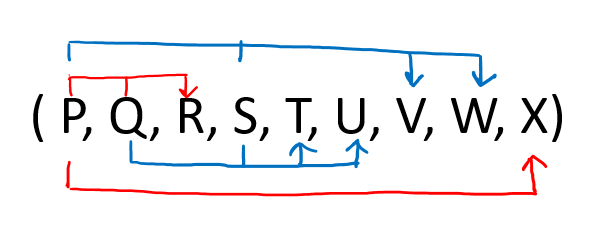 Since R has 5 attributes: - P, Q, R, S, T and Candidate Keys are RS and RQ, Therefore prime attributes (part of candidate key) are S Q R while a non-prime attribute is TP Given FD are { QR → PST, S → Q } and Super Key / Candidate Key is RS and RQ NOTE: To solve such questions, we apply reverse engineering, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.
Since there were only two FD's, out of which one ( QR → PST ) satisfy BCNF while the other ( S → Q) satisfy 3NF, hence the highest normal form is 3NF R(P, Q, R, S, T) is in 3NF. Question 5: Given a relation R( A, B, C) and Functional Dependency set FD = { A → B, B → C, and C → A}, determine given R is in which normal form? Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key. 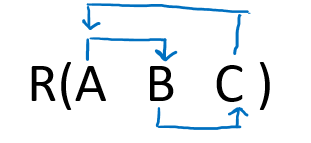 From the above arrow diagram on R, we can see that all the attributes are determined by all the attributes of the given FD, hence we will check all the attributes (i.e., A, B, and C) for candidate keys Let us calculate the closure of A A + = ABC (from the closure method we studied earlier) Since closure A contains all the attributes of R, hence A is the Candidate key. Let us calculate the closure of B B + = BAC (from the closure method we studied earlier) Since closure B contains all the attributes of R, hence B is the Candidate key. Let us calculate the closure of C C + = CAB (from the closure method we studied earlier) Since closure C contains all the attributes of R, hence C is the Candidate key. Hence three Candidate keys are: A B and C Since R has 3 attributes: - A B and C, Candidate Keys are A B and C, Therefore, prime attributes (part of candidate key) are A B C while there is no non-prime attribute Given FD are { A → B, B → C, and C → A } and Super Key / Candidate Key is A B and C NOTE: To solve such questions, we apply reverse engineering, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.
Since there were only three FD's and all FD: { A → B, B → C and C → A } satisfy BCNF, hence the highest normal form is BCNF. Therefore R(A, B, C ) is in BCNF. Conclusion: From the above three examples, we can conclude that the following steps are followed to identify the normal form for a given relational schema. STEP 1: Calculate the Candidate Key of given R by using an arrow diagram and then using the closure of an attribute on R, such that from the calculated candidate key we can separate the prime attributes and non-prime attributes. STEP 2: Verify each FD's in the reverse engineering process, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on. STEP 3: If a table is in BCNF then it is in 3NF, 2NF, and 1NF, similarly if the table is in 3NF THEN it is in 2NF and 1NF. Hence, we can say that if a table is in the higher normal form then by default it is in lower normal form. STEP 4: Verify first FD with Definition of BCNF (First it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then X is Super Key. STEP 5: If for any FD STEP 5 fails(it signifies that table is not in BCNF), then verify that FD and remaining FD with Definition of 3NF( First it should be in 2NF and if there exist a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then X is Super Key or Y is a prime attribute STEP 6: If for any FD STEP 6 fails (it signifies that table is not in BCNF), then verify that FD and remaining FD with Definition of 2NF (No non-prime attribute should be partially dependent on the key of table). STEP 7: If for any FD STEP 7 fails (it signifies that table is not in 2NF), hence no need to check it for 1NF, as by default it is in 1NF. STEP 8: If all the FD's satisfy the definition of BCNF then we can say that given R is in BCNF, if any FD fails for BCNF and that FD and remaining FD satisfy for 3NF then we say R is in 3NF, similarly if any FD fails for 3NF and that FD and remaining FD satisfy for 2NF then we say R is in 2NF, otherwise the table is in 1NF. Next TopicTypes of Relationship in Database Table
|