A one-way ANOVA (“analysis of variance”) is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups.
This tutorial explains how to perform a one-way ANOVA in Excel.
Example: One-Way ANOVA in Excel
Suppose a researcher recruits 30 students to participate in a study. The students are randomly assigned to use one of three studying techniques for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same test.
The test scores for the students are shown below:

The researcher wants to perform a one-way ANOVA to determine if the average scores are the same across all three groups.
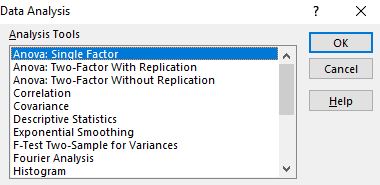
To perform a one-way ANOVA in Excel, navigate to the Data tab, then click on the Data Analysis option within the Analysis group.
If you don’t see the Data Analysis option, then you first need to load the free Analysis ToolPak.
Once you click this, a window will pop up with different Analysis Tools options. Select Anova: Single Factor, then click OK.
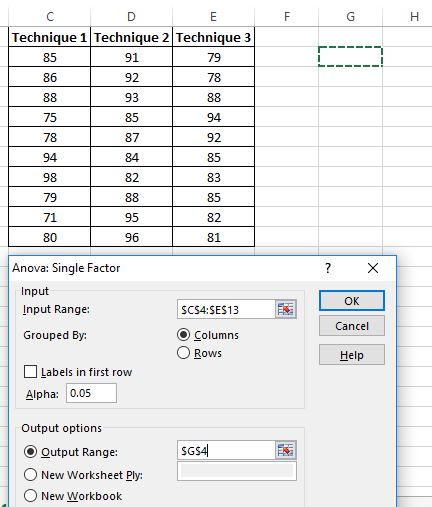
A new window pops up asking for an Input Range. You can either drag a box around your data or manually enter the data range. In this case, our data is in cells C4:E13.
Next, choose an Alpha level for the test. By default, this number is 0.05. In this case, I’ll leave it as 0.05.
Lastly, choose a cell for the Output Range, which is where the results of the one-way ANOVA will appear. In this case, I choose cell G4.
Once you click OK, the output of the one-way ANOVA will appear:
Interpreting the Output
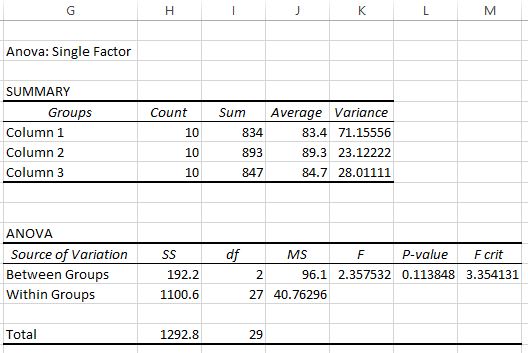
There are two tables shown in the output. The first is a summary table, which shows the count of test scores in each group, the sum of the test scores, the average of the test scores, and the variance of the test scores.
Recall that a one-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more groups.
From this first table, we can see that the mean score for each of the three groups is different, but to know if these differences are statistically significant, we need to look at the second table.
The second table shows the F test statistic, the F critical value, and the p-value:

In this case the F test statistic is 2.3575 and the F critical value is 3.3541. Since the F test statistic is less than the F critical value, we do not have sufficient evidence to reject the null hypothesis that the means for the three groups are equal.
This means we do not have sufficient evidence to say that there is a difference in test scores among the three studying techniques.
We could also use the p-value to reach the same conclusion. In this case the p-value is 0.1138, which is greater than the alpha level of 0.05.
This means we do not have sufficient evidence to reject the null hypothesis that the means for the three groups are equal.
Note: In cases where you do reject the null hypothesis, you can perform a Tukey-Kramer post hoc test to determine exactly which group means are different.